Danes bomo spoznali, kako lahko trikotniku včrtamo krožnico. Najprej v zvezek prepiši naslov in nariši večji ostrokotni trikotnik. Nariši simetrale vseh treh notranjih kotov. Hitro lahko ugotoviš, da se simetrale sekajo v skupni točki. To je središče trikotniku včrtane krožnice, ki ga označimo Sv. Na eno stranico trikotnika nariši pravokotnico do središča. Narisal si polmer trikotniku včrtane krožnice, ki ga označimo z rv. V roke vzemi šestilo in poskusi narisati krožnico. Pri načrtovanju si lahko pomagaš s POSNETKOM. 

Če si bil pri načrtovanju trikotnika dovolj natančen, si narisal takšno sliko:

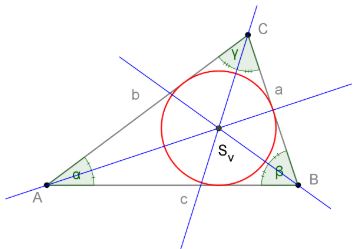
V zvezek prepiši: 

Točka Sv, ki je enako oddaljena od vseh treh stranic trikotnika, je središče trikotniku včrtane krožnice. Je presečišče simetral vseh treh notranjih kotov trikotnika. Razdalja točke Sv od poljubne stranice je polmer včrtane krožnice rv.

Na spletni strani premikaj oglišča trikotnika in spreminjaj trikotnike: GEOGEBRA.

V delovnem zvezku na straneh 48, 49 reši naloge 1, 2 ter 3 a in b primer. Za dodatno vajo lahko rešiš še ostale primere pri 3. nalogi.